前言：
「梯度不穩定」（unstable gradient）是我們在深度學習或機器學習中，訓練模型時遇到的一種問題，當我們的隱藏層越來越多就可能會遇到。

梯度不穩定

梯度不穩定其中又分為兩種：

1. 梯度消失（Gradient Vanishing）： 在深度神經網路中，因為用反向傳播計算損失函數對權重的梯度會碰到鏈鎖律的操作。如果相乘的導數絕對值都是小於1的話，那結果就會用指數的速度靠近0，例如：sigmoid的梯度值範圍是0~0.25，假設我們隱藏層有10層，算梯度要乘上10次sigmoid的梯度值（0.25^10），乘起來權重梯度值會非常靠近0。總結一句：因為是反向傳播，離輸 出 層最近的會先算，連鎖律乘到最後，離輸入最近的那幾層將會因為梯度趨近於0(消失)而停滯學習，這種情況叫做梯度消失。

2. 梯度爆炸（Gradient Explosion）： 梯度爆炸並沒有梯度消失那麼常見，簡單來看可以視為梯度消失的相反。當許多導數絕對值都大於1時，計算損失函數對權重的梯度就會像指數一樣的膨脹，使得更新的步伐跨太大，導致損失一直在震盪。在反向傳播過程中，權重更新變得極端，使模型變得不穩定，難以訓練。

解決梯度不穩定性的方法包括：

• 激活函數選擇（Activation Function Choice）-Day10
• 損失函數設計（Loss Function Design）- Day13
• 批樣本大小（Batch Size）-Day16
• 學習率調整（Learning Rate Scheduling）-Day16
• 權重初始化（Weight Initialization）-Day19
  最後還有一個正則化（Regularization） 也就是我們今天的主角

正規化&批次正規化

通常批次正規化可以幫助我們加速訓練收斂速度、減輕梯度爆炸和梯度消失、減少對權重初始化的敏感也可以提高模型的穩定性，不過即使批次正規化在許多情況下都能提升模型效能，但並非適用於所有情況。在一些特定的架構中，批次正規化可能會導致效能下降，或需要進行一些調整。因此，在決定是否使用批次正規化時，我們還是要根據具體情況進行實驗和評估。

正規化（Normalization）：
正規化是一種用於資料的預處理技術，讓每種特徵值都使用相同的計量標準。將資料縮放到相對較小的範圍內，且不改變其原本分佈，通常在0到1或-1到1之間。

批次正規化（Batch Normalization，BN）：
批次正規化可以幫助我們加速訓練神經網路並減輕梯度爆炸或梯度消失的問題。批次正規化針對「神經層的輸出值」做處理，其主要想法是在每個神經網路層的輸入上進行正規化（如圖1），經過轉換後就會是「平均值為0，標準差為1」的分佈了（如圖2）

圖1

圖2
簡單來說就是把偏離的紅色或藍色變成黑色虛線，也可以稱之為標準化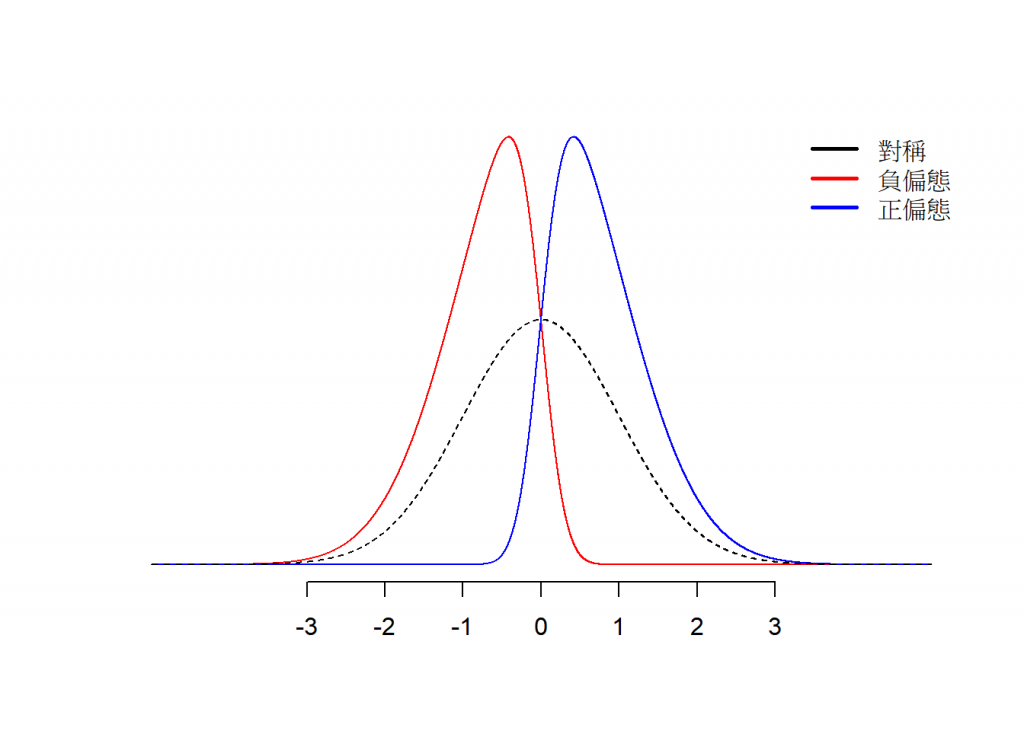

資料來源：https://bookdown.org/ccwupsy/data-analysis/statistics.html
查找日期：2023/10/02